Notice
Recent Posts
Recent Comments
Link
스토리지
[4.1] Binary Search Tree 이진탐색트리 본문
정의
- 왼쪽 노드의 값이 루트 노드의 값보다 작고, 오른쪽 노드의 값이 루트 노드의 값보다 큰 이진트리.
- 왼쪽에서 오른쪽으로 갈 수록 크므로 정렬되어 있다.
- Add연산의 경우, 알아서 자기가 위치할 자리를 찾아간다.
예시코드
using System;
namespace Study03
{
public class Node
{
public int data;
public Node left;
public Node right;
public Node(int data)
{
this.data = data;
}
}
public class BSTree
{
private Node root;
public BSTree()
{
}
public void Add(int data)
{
if(root == null)
{
root = new Node(data);
return;
}
Node node = root;
while(node != null)
{
if(node.data == data)
{
throw new ApplicationException("Duplicated data.");
}
else if(data > node.data)
{
if(node.right == null)
{
node.right = new Node(data);
break;
}
node = node.right;
}
else
{
if(node.left == null)
{
node.left = new Node(data);
break;
}
node = node.left;
}
}
}
//Iterator를 통한 Binary Search Tree 탐색
public Node Search(int data)
{
Node discover = this.root;
while (discover != null)
{
if (discover.data == data)
return discover;
if (discover.data > data)
{
discover = discover.left;
}
else
{
discover = discover.right;
}
}
return null;
}
public bool SearchRecursive(int data)
{
return SearchRecursive(this.root, data);
}
//재귀를 통한 Binary Search Tree 탐색
public bool SearchRecursive(Node node, int data)
{
if (node == null) return false;
if (node.data == data) return true;
return SearchRecursive(node.left, data) || SearchRecursive(node.right, data);
}
public void PrintPreorder()
{
Preorder(this.root);
Console.WriteLine();
}
private void Preorder(Node node)
{
if (node == null) return;
Console.Write("{0} ", node.data);
Preorder(node.left);
Preorder(node.right);
}
}
}using System;
namespace Study03
{
public class App
{
public App()
{
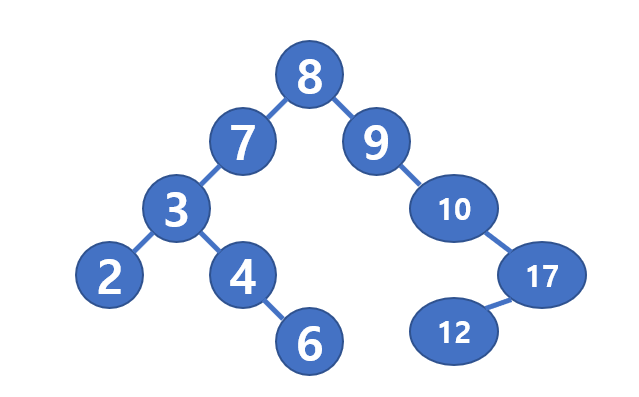
BSTree tree = new BSTree();
tree.Add(8);
tree.Add(7);
tree.Add(9);
tree.Add(3);
tree.Add(2);
tree.Add(4);
tree.Add(10);
tree.Add(17);
tree.Add(12);
tree.Add(6);
tree.PrintPreorder();
Node node = tree.Search(12);
if(node != null)
{
Console.WriteLine("Yes {0}", node.data);
}
else
{
Console.WriteLine("Can't find in tree");
}
}
}
}
삭제연산
- 자식노드가 없을때
부모로부터 잘라주기만 하면됨.
- 자식노드가 하나만 있을때
삭제하려는 노드의 부모 아래에 자식을 두게하면 된다.
- 자식노드가 두 개 있을 때
삭제하려는 노드를 기준으로 왼쪽 서브트리의 가장 오른쪽에 있는 값 혹은 오른쪽 서브트리의 가장 왼쪽에 있는 값을 삭제하려는 노드에 복사해주고 복사당한 노드는 삭제한다.
( ∵ 트리의 형태를 유지하기 위해서 )
'Unity > 자료구조' 카테고리의 다른 글
| [4.2] Graph 1 (0) | 2021.04.02 |
|---|---|
| [4.2] Binary Search Tree 복습 (0) | 2021.04.02 |
| [4.1] Binary Tree Traversal 복습 (0) | 2021.04.01 |
| [3.31] Binary Tree Preorder 연습 (0) | 2021.03.31 |
| [3.31] Binary Tree 연습 1 (Array) (0) | 2021.03.31 |
Comments




